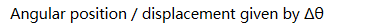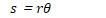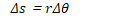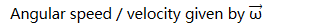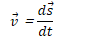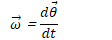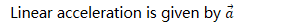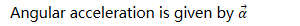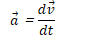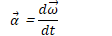Radians and Degrees

  • In degrees, once around a circle is 360°

  • In radians, once around a circle is 2π

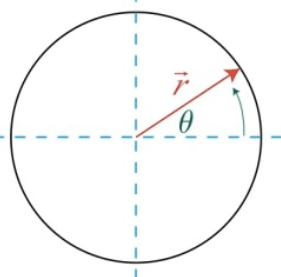
  • A radian measures a distance around an arc equal to the length of the arc's radius

  • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image026.png

Linear vs. Angular Displacement

C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image027.png

  • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image028.png

  • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image029.png

  • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image030.png

  • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image031.png

Linear vs. Angular Velocity

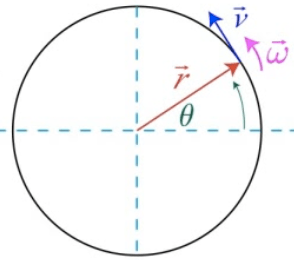
C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image032.png

  • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image033.png

  • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image034.png

  • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image035.png

  • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image036.png

Direction of Angular Velocity

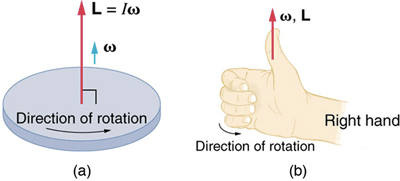
L = 10) irection of rotati Right hand Direction of rotation

Converting Linear to Angular Velocity

C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image038.png

Linear vs. Angular Acceleration

C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image039.png

  • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image040.png

  • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image041.png

  • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image042.png

  • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image043.png

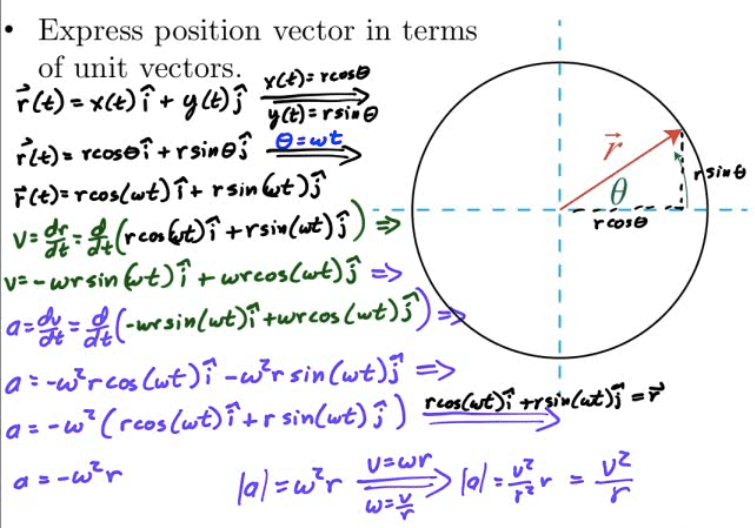
Centripetal Acceleration

Express position vector in terms of unit vectors. Fte)z r$in a —Jr sin

Reference Frames

  • A reference frame describes the motion of an observer

    • Most common reference frame is Earth

  • Laws of physics we study in this course assume we're in an inertial, non-accelerating reference frame

  • There is no way to distinguish between motion at rest and motion at a constant velocity in an inertial reference frame

Calculating Relative Velocities

  • Consider two objects, A and B.

  • Calculating the velocity of A with respect of reference frame B (and vice versa) is straightforward

  • Example:

    • Speed of car with respect to the ground

    • Walking on a train, speed of a person with respect to the train

  • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image045.png

Linear vs. Angular

Rotational Motion (a = constant) 0=00 -Fat = — (00 + e = + —at2 02 = + 2a9 Linear Motion (a = constant) v vo + at vot + —at 2 2 = v: + 2ax

results matching ""

    No results matching ""